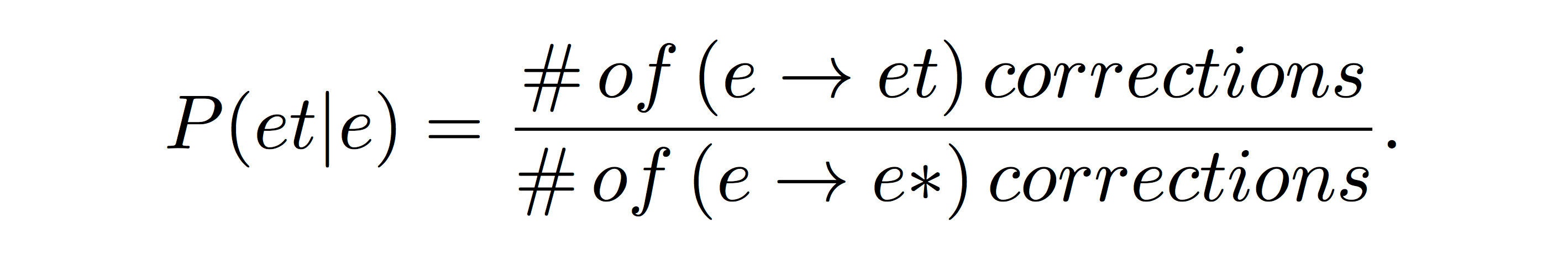Modeling Spelling Correction for Search at Etsy
Introduction
When a user searches for an item on Etsy, they don't always type what they mean. Sometimes they type the query jewlery when they're looking for jewelry; sometimes they just accidentally hit an extra key and type dresss instead of dress. To make their online shopping experience successful, we need to identify and fix these mistakes, and display search results for the canonical spelling of the actual intended query. With this motivation in mind, and through the efforts of the Data Science, Linguistic Tools, and the Search Infrastructure teams, we overhauled the way we do spelling correction at Etsy late last year.
The older service was based on a static mapping of misspelled words to their respective corrections, which was updated only infrequently. It would split a search query into its tokens, and replace any token that was identified as a misspelling with its correction. Although the service allowed a very fast way of retrieving a correction, it was not an ideal solution for a few reasons:
- It could only correct misspellings that had already been identified and added to the map; it would leave previously unseen misspellings uncorrected.
- There was no systematic process in place to update the misspelling-correction pairs in the map.
- There was no mechanism of inferring the word from the context of surrounding words. For instance, if someone intended to type butter dish, but instead typed buttor dish, the older system would correct that to button dish since buttor is a more commonly observed misspelling for button at Etsy.
- Additionally, the older system would not allow one-to-many mappings from misspellings to corrections. Storing both buttor -> button and buttor -> butter mappings simultaneously would not be possible without modifying the underlying data structure.
We, therefore, decided to upgrade the spelling correction service to one based on a statistical model. This model learns from historical user data on Etsy’s website and uses the context of surrounding words to offer the most probable correction.
Although this blog post outlines some aspects of the infrastructure components of the service, its main focus is on describing the statistical model used by it.
Model
We use a model that is based upon the Noisy Channel Model, which was historically used to infer telegraph messages that got distorted over the line. In the context of a user typing an incorrectly spelled word on Etsy, the “distortion” could be from accidental typos or a result of the user not knowing the correct spelling. In terms of probabilities, our goal is to determine the probability of the correct word, conditional on the word typed by the user. That probability, as per Bayes’ rule, is proportional to the product of two probabilities:
We are able to estimate the probabilities on the right-hand side of the relation above, using historical searches performed by our users. We describe this in more detail below.
To extend this idea to multi-word phrases, we use a simple Hidden Markov Model (HMM) which determines the most probable sequence of tokens to suggest as a spelling correction. Markov refers to being able to predict the future state of the system based solely on its present state. Hidden refers to the system having hidden states that we are trying to discover. In our case, the hidden states are the correct spellings of the words the user actually typed.
The main components of an HMM are explained via the figure below. Assume, for the purpose of this post, that the user searched for Flower Girl Baske when they intended to search for Flower Girl Basket. The main components of an HMM are then as follows:
- Observed states: the words explicitly typed by the user, Flower Girl Baske (represented as circles).
- Hidden states: the correct spellings of the words the user intended to type, Flower Girl Basket (represented as squares).
- Emission probability: the conditional probability of observing a state given the hidden state.
- Transition probability: the probability of observing a state conditional upon the probability of the immediately previous observed state, like, for instance, in the figure below, the probability of transitioning from Girl to Baske, i.e., P(Baske|Girl). The fact that this probability does not depend on the probability of having observed Flower, the state that precedes Girl, illustrates the Markov property of the model.
Once the spelling correction service receives the query, it first splits the query into three tokens, and then suggests possible corrections for each of the tokens as shown in the figure below.
In each column, one of the correction possibilities represents the true hidden state of the token that was typed (emitted) by the user. The most probable sequence can be thought of as identifying the true hidden state for each token given the context of the previous token. To accomplish this, we need to know probabilities from two distributions: first, the probability of typing a misspelling given the correct spelling of the word, the emission probability, and, second, the probability of transitioning from one observed word to another, the transition probability.
Once we are able to calculate all the emission probabilities, and the transition probabilities needed, as described in the sections below, we can determine the most probable sequence using a common dynamic programming algorithm known as the Viterbi Algorithm.
Error Model
The emission probability is estimated through an Error Model, which is a statistical model created by inferring historical corrections provided by our own users while making searches on Etsy. The heuristic we used is based on two conditions: a user’s search being followed immediately by another search similar to the first, and with the second search then leading to a listing click. We align these tokens to each other in a way that minimizes the number of edits needed on the misspelled query to transform it into the corrected second query.
We then make aligned splits on the characters, and calculate counts and associated conditional probabilities. We generate character level probabilities for four types of operations: substitution, insertion, deletion, and transposition. Of these, insertion and deletion also require us to also keep track of the context of neighboring letters -- the probability of adding a letter after another, or removing a letter appearing after another, respectively. To continue with the earlier example, when the user typed baske, the emitted token, they were probably trying to type basket, the hidden state for baske, which corresponds to the probability P(Baske|Basket). Error probabilities for tokens, such as these, are calculated by multiplying the character-level probabilities which are assumed to be independent. For instance, the probability of correcting the letter e by appending the letter t to it is given by:
Here, the numerator is the number of times in our dataset where we see an e being corrected to an et, and the denominator is the number of corrections where any letter was appended after e. Since we assume that the probability associated with a character remaining unchanged is 1, in our case, the probability P(Baske|Basket) is solely dependent on the insertion probability P(et|e).
Language Model
Transition probabilities are estimated through a language model which is determined by calculating the unigram and bigram token frequencies seen in our historical search queries.
A specific instance of that, from the chosen example, would be the probability of going from one token in the Flower (first) column, say Flow, to a token, say Girl, in the Girl (second) column, which is represented as P(Girl|Flow). We are able to determine that probability from the following ratio of bigram token counts to unigram token counts:
The error models and language models are generated through Scalding-powered jobs that run on our production hadoop cluster.
Viterbi Algorithm Heuristic
To generate inferences using these models, we employ the Viterbi Algorithm to determine the optimal query, i.e., sequence of tokens to serve as a spelling correction. The main idea is to present the most probable sequence as the spelling correction. The iterative process goes, as per the figure above, from the first column of tokens to the last. At the nth iteration, we have the sequence with the maximum probability available from the previous iteration, and we choose the token from the nth column which increases the maximum probability from the previous iteration the most.
Let’s explain this more concretely by describing the third iteration for our main example: assume that we already have Flower girl as the most probable phrase at the second iteration. Now we pick the token from the third column that corresponds to the maximum of the following transition probability and emission probability products:
We can see from the figure above that the transition probability from Girl to Basket is high enough to overcome the lower emission probability of someone typing Baske when they mean to type Basket, and that, consequently, Basket is the word we want to add to the existing Flower Girl phrase.
We now know that Flower Girl Basket is the most probable correction as predicted by our models. The decision about whether we suggest this correction to the user, and how we suggest it, is made on the basis of its confidence score. We describe that process a little later in the post.
Hyperparameters and Model Training
We added a few hyperparameters to the bare bones model we have described so far. They are as follows:
- We added an exponent to the emission probability because we want the model to have some flexibility in weighting the error model component in relation to the language model component.
- Our threshold for offering a correction is a linear function of the number of tokens in the query. We, therefore, have a slope and the intercept of the threshold as a pair of hyperparameters.
- Finally, we also have a parameter corresponding to the probability of words our language model does not know about.
Our training data set consists of two types of examples: the first kind are of the form misspelling -> correct spelling, like jewlery -> jewelry, while the second kind are of the form correct spelling -> , like dress -> . The second type corresponds to queries that are already correct, and therefore don’t need a correction. This setup enables our model to distinguish between the populations of both correct and incorrect spellings, and to offer corrections for the latter.
We tune our hyperparameters via 10-fold cross-validation using a hill-climbing algorithm that maximizes the f-score on our training data set. The f-score is the harmonic mean of the precision and the recall. Precision measures how many of the corrections offered by the system are correct and, for our data set, is defined as:
Recall is a measure of coverage -- it tries to answer the question, “how many of the spelling corrections that we should be offering are we offering?”. It is defined as:
Optimizing on the f-score is allows us to increase coverage of the spelling corrections we offer while keeping the number of invalid corrections offered in check.
Serving the Correction
We serve three types of corrections at Etsy based on the confidence we have in the correction. We use the following odds-ratio as our confidence score:
If the confidence is greater than a certain threshold, we display search results corresponding to the correction, along with a "Search instead of" link to see the results for the original query instead. If the confidence is below a certain threshold, we offer results of the original query, with a “Did you mean” option to the suggested correction. If we don’t have any results for the original query, but do have results for the corrected query, we display results for the correction independent of the confidence score.
Spelling Correction Service
With the new service in place, when a search is made on Etsy, we fire off requests to both the new Java-based spelling service and the existing search service. The response from the spelling service includes both the correction and its confidence score, and how we display the correction, based on the confidence score, is described in the previous section. For high-confidence corrections, we make an additional request for search results with the corrected query, and display those results if their count is greater than a certain threshold.
When the spelling service receives a query, it first splits it into its constituent tokens. It then makes independent suggestions for each of the tokens, and, finally, strings together from those suggestions a sequence of the most probable tokens. This corrected sequence is sent back to the web stack as a response to the spelling service request.
The correction suggestions for each token are generated by Lucene’s DirectSpellChecker class which queries an index generated from tokens that are generated through a Hadoop job. The Hadoop job counts tokens from historical queries, rejecting any tokens that appear too infrequently or those that appear only in search queries with very few search results. We have a daily cron that ships the tokens, along with the generated Error and Language model files, from HDFS to the boxes that host the spelling correction service. A periodic rolling restart of the service across all boxes ensures that the freshest models and index tokens are picked up by the service.
Follow-up Work
The original implementation of the model was limited, in the sense, that it could not suggest corrections that were, at the token level, more than two edits away from the original token. We have subsequently implemented an auxiliary framework of suggesting correction tokens that fixes this issue.
Another limitation was related to splitting and compounding of tokens in the original query to make suggestions. For instance, we were not able to suggest earring as a suggestion for ear ring. Some of our coworkers are working on modifying the service to accommodate corrections of this type.
Although we do use supervised learning to train the hyperparameters of our models, since launching the service we have additional inputs from our users which we can improve our models with. Specifically, users clicking the “Did you mean” link on our low-confidence corrections results page provides us with explicit positive feedback, while clicks on the “Search instead for” link on our high-confidence corrections results page provides us with negative feedback. The next major evolution of the model would be to explicitly use this feedback to improve corrections.
(This project was a collaboration between Melanie Gin and Benjamin Russell on the Linguistic Tools team who built out the infrastructure and front-end; Caitlin Cellier and Mohit Nayyar on the Data Science team who worked on implementing the statistical model; and Zhi-Da Zhong on the Search Infrastructure team who consulted on infrastructure design. A special thanks to Caitlin whose presentation some of these figures are copied from.)